MOP is a flexible multi-solver framework intended to be fast, customizable and modular. The project was born because of my desire to unify the amount of redundancy and sensitivity I read in scientific papers. E.g: Articles written with the same solver and problem instance had very distant results due to one or two different parameters or a slight and specific modification of a well-known problem sometimes led to significant adaptations.

A flexible mathematical optimization program is nothing new, there are many better projects out there, MATLAB, Ensmallen and Ceres are some examples but MOP is written in Rust, a systems programming language that is fast, productive and much safer than similar alternatives.

NP-Problems

One of the reasons why it is very hard to find feasible solutions for Non-deterministic Polynomial Problems are due to their large search spaces. Take for example the classic Traveling Salesman problem (TSP), the set S of all possible traveling combinations is N! with N being the number of cities. Now imagine an instance with 80 cities, then S will be equal to 7,156945705×10¹¹⁸ and no supercomputer in the world will be able to brute-force every combination of this set that is much greater than the number of atoms or the age of the universe.

Curiously, it is not mathematically proven if P≠NP or P=NP

Luckily, there are a lot of methods that can find optimal or sub-optimal (good enough) solutions in a reasonable/efficient time. In fact, there are a lot of different methods divided in several fields and each field is probably complex enough to deserve a new PhD thesis. To name a few: Linear/Quadratic programming and Heuristics/Meta-heuristics.

Architecture

In face of so many distinct problems and solvers, MOP tries to follow the philosophy of grouping them into common interfaces and structures for easier implementation, interoperability and analysis.

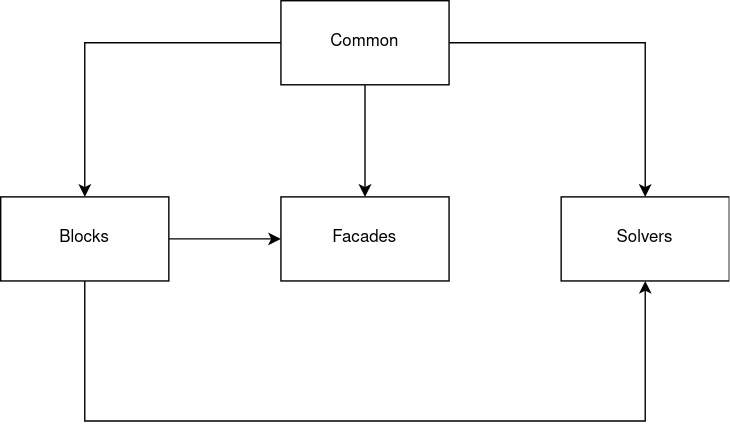
• Blocks: Structures to storage and evaluate problems definitions and results.
• Common: Common code used across all crates.
• Facades: The user front-end that glues different problems and solvers through the Solver trait.
• Solvers: Optional crate that provides built-in solvers.

What brings together this architecture is undoubtedly the Solver trait.

pub trait Solver<P> { // Type `P` for Problem
  fn after_iter<'a>(&'a mut self, p: &'a P) -> SolverFuture<'a>;

  fn before_iter<'a>(&'a mut self, p: &'a P) -> SolverFuture<'a>;

  fn finished(&mut self, _: &mut P) {}

  fn init(&mut self, _: &mut P) {}
}

Any solver, not just the ones defined in the Solvers crate, that implements the Solver trait can be used to solve a problem P through one of the Facades user's interfaces.

Changes

The way things are structured today might change in the future to better accommodate new general ideas or enhancements. Nevertheless, I will try to keep the following guidelines.

• Flexible: Specify any type of solver combination/sequence and its related parameters to drive the optimization of any supported problems.
• Modular: Isolate singular responsibilities, expand functionalities and share common code for internal and external development.
• Solvers: Provide built-in heterogeneous solvers and not be restricted to a single methodology. The possibilities are many: Meta-heuristic solvers, SAT solver or nonlinear programming solvers.
• Problems: Be able to construct continuous or discrete problems, single or multi objectives, constrained or non-contained. E.g.: Scheduling problems, Rastrigin function, Vehicle Routing Problem, Rosenbrock function and Cutting Stock Problem.

Results

Although one of the principles of this project is to host several solvers, there is currently only one available, SPEA2 (Zitzler et al., 2001), which is a meta-heuristic genetic algorithm. Its performance and quality will be measured against Binh and Korn, a problem composed of two hard constraints and two objectives with the respective reference results available on this Wikipedia page.

All tests were performed in my workstation, a notebook with Intel i5 72000U and 8GB memory. The code is a gist hosted at https://gist.github.com/c410-f3r/4285385cd780652d6bf068b2750da170.

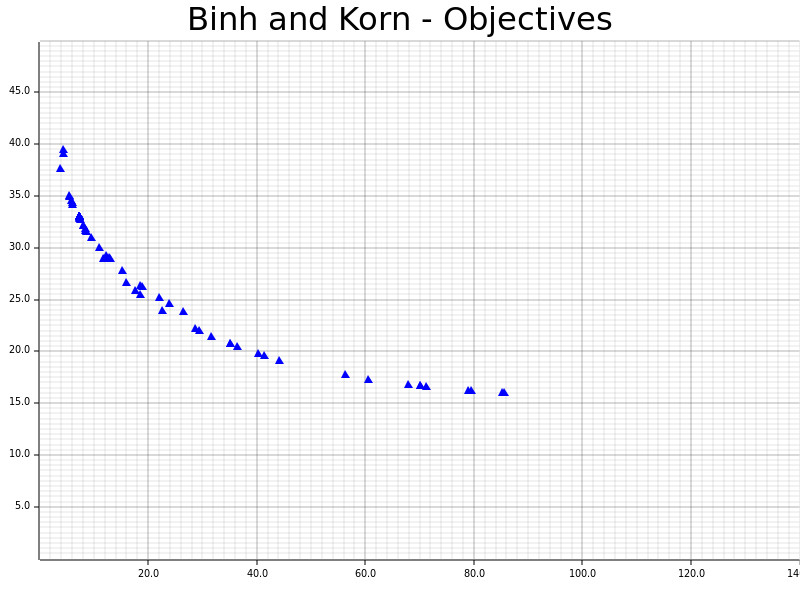
You can see the Pareto front where the objectives results were very similar to the ones found on Wikipedia. Two main things regarding the solver and its parameters are noteworthy: First, there are more solutions at the top than at the bottom of the graph indicating a possible elitism. Two, some off-the-line solutions are probably indicating an intentional algorithm diversification for a better search-sparse exploration and off-springs.

The execution speed is very fast, a mean of 0.2 seconds across 11 runs.

Unfortunately, the current solver isn't so good for other problems. This temporary limitation will be explored with more details in a next post.

Final words

For those wondering about the possibility of using this library, I personally would recommend the usage of the similar alternatives described in the beginning of this post. Many things can or could be improved and despite years of personal research, development and headaches, this whole thing is still a hobbyist adventure.